PS:
最近在做机器学习的笔记, 我是按照自己的体会将机器学习 里某一块的知识点进行具体介绍,有新的补充都会在原文进行添加,欢迎评论,分享(仅限于非商业性转载,且注明出处)。
Abstract:
无论是概率统计还是机器学习,贝叶斯都是迈不出去的一道坎,这里总结下自己的学习笔记,很多东西我自己理解的也不深,这里我尽量用浅显的方式去表达。
什么是概率学
生活中其实处处都是不确定的东西,明天是天晴还是下雨?这个项目成功的可能性有多少?隔壁老王明天会穿黑色还是蓝色衣服来上班?好吧,职业病! 这个产品在亚马逊平台成为爆款的可能性会有多少?… 这些问题通常都认为是随机的,但是呢,事实上任何事情都是跟其他事情有千丝万缕的关系,概率论就是研究事情关联关系的一门学问,概率论是应用数学的 一个重要分支, 广泛应用于日常生活中,它起源于十七世纪,据说那些大神们开始研究概率的问题,只是开始于赌博的研究,后来才发展到社会的方方面面,事实上在Data-Driven的今天,它已经是商科必修的一门学科。
贝叶斯实列1:生病的几率
某人被发现有一些症状,所以作为预防措施,医生会采取血液样本,看看患者是否患有某种罕见容易致死的疾病。患者被告知检测出现阳性,病人显然会非常担心,我想我们中的任何一个人都会非常担心,因为检测结果呈现阳性,而且这种病很可能会致死。
医生告诉我们,每10,000人中只有一人患有这种疾病。医生还告诉患者,如果您有感染,那么您有99%的可能会检测出该病的阳性。未受感染的怎么样? 2%的未感染患者仍将检测出该病的阳性。换句话说,2%的健康患者仍然会检测出现阳性。如果这种罕见疾病检测呈现阳性,那么我的检测结果可以推测出生病的概率是多少?
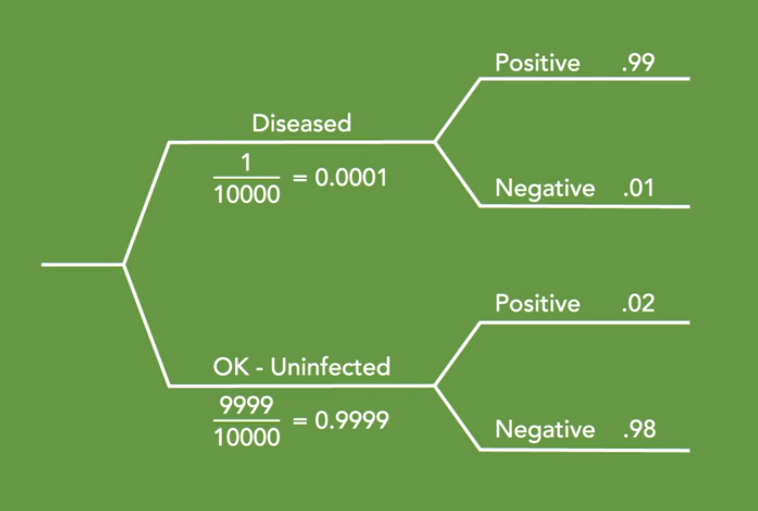
为此,让我们使用概率树。我们正在研究两个不同的事件。事件A,患者患有此病。事件B,患者对该疾病检测呈阳性。
事件一,患者是否患有这种疾病?如果1个人得病,那么剩下的9999人不会得病。所以我们患病的分支的值为0.0001。我们健康的分支值为0.9999。然后我们可以继续前进到第二个事件。患者检测呈阳性吗?对于实际患有该疾病的患者,99%的检测阳性和1%的患有实际疾病的患者将检测为阴性。
对于那些没有患病的患者,98%将检测为阴性,0.98,但2%将检测为阳性,0.02。这些是误报的人。让我们计算每个分支的价值。检测阳性的患病患者的可能性是0.0001*0.99,这给我们0.000099。
检测阴性的患病患者的价值是0.0001 0.01,这给了我们0.0000001, 这是个微小的数字。检测阳性的健康患者的价值是0.9990.98,这给了我们0.979902。测试阴性的健康患者的价值是0.999*0.02,这给我们0.019998。
那么这是什么意思?在一个拥有100万人口的城市中,有100人实际上患有这种疾病。在这100个人中,99个将测试为阳性,一个人将进行阴性测试,而不是发现他们患有这种疾病。这也意味着在一百万人中,有999,900人不会患上这种疾病,但在那些没有患病的999,900人中,19,998人将得到一个阳性的测试结果。
最后,回到我们的问题。如果我测试为阳性,我应该多担心?在100万人中,有20,097人将检测出阳性结果,但这些人中只有99人会患上这种疾病。因此,如果你测试为阳性,那么实际患病的可能性为0.5%。换句话说,每200名对该疾病检测呈阳性的人中,只有一人确实患有这种疾病。
实际上,即使检测出来是阳性,我们也只有0.05%的可能性得病,不用非常担心,这比之前我们预计的可能性要小很多,不是吗?我们在这里所做的是我们称之为贝叶斯定理的基础。它不仅有趣,而且非常有用。
贝叶斯实列2:富人跟学历的关系:
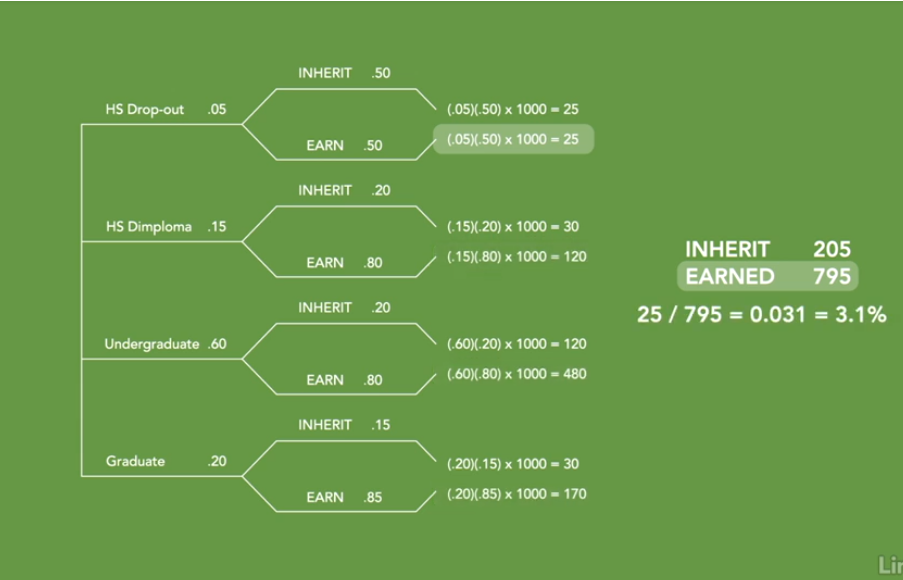
这个问题是研究富人是如何致富的?好吧,假使我们有这组数据。某个国家的富翁20%有研究生学位, 60%的本科学位, 15%的人只有高中文凭, 5%的人甚至没有完成高中学业. 当然有一部分富翁是继承了财富。以下是数据:高中辍学的百万富翁中有50%继承了他们的财富,拥有高中文凭或本科学位的百万富翁中有20%继承了他们的财富。而且,只有15%拥有研究生学位的百万富翁继承了他们的财富。那么靠自己能力赚取财富成为富翁是高中生的几率是多少呢?让我们建立一棵树。
我们的第一组分支机构确立了教育水平。然后,我们的第二组分支机构将这些不同类型的富翁分解为那些继承财富的人和那些赚取财富的人。通过将第一个分支的值乘以第二个分支的值,我们可以看到每个结果的概率。简化:假设有1000位富翁。我们可以将每个分支值乘以1000。
我们现在可以看到每个类别中有多少富翁。例如,有200名百万富翁拥有研究生学位,170名是自己赚的钱,30名继承了家业。我们还可以看到,1000名百万富翁中的795人靠自己赚的钱。在那些795中,25名没有高中毕业。
通过划分这两个数字,我们现在可以看到富翁没有完成高中的概率,是3.1%。有些人可能想知道有没有方法可以在没有图表的情况下做到这一点?有。贝叶斯定理的公式如下所示。

我知道,这公式看起来有点难看,相对于这个问题,分子是高中生致富的人数,分母是各种学历自己致富的总人数。分母看起来很丑陋,但它真的只是试图将所有靠自己赚钱各种学历的人根据提供的百分比数据加起来。所以在这里我们将辍学率概率乘以5%,辍学率为50%。
因此,无论您是在查看误报数据,犯罪数据,教育数据,科学数据,还是商业数据,贝叶斯定理都可以帮助您了解关系和概率。
理解贝叶斯公式
假设 P(Ai|B)是我们想知道的概率,这里叫做后验概率,而这个概率就是贝叶斯统计中的 后验概率!而人群中患癌症与否的概率 P(A1),P(A2),就是 先验概率!各个学历自己致富的概率也是先验概率,我们知道了先验概率,根据观测值(observation),也可称为test evidence:是否为阳性(Positive),来判断得癌症或者致富的的后验概率,这就是基本的贝叶斯思想。
贝叶斯与频率学派
频率学派跟贝叶斯学派打架的历史很悠久,频率学派重视数据,而贝叶斯派重视先验,也就是主观感受
贝叶斯学派重视先验
频率学派重视似然,
首先来看似然函数 f(x|θ),似然函数听起来很陌生,其实就是我们在概率论当中看到的各种概率分布 f(x),那为什么后面要加个参数 |θ 呢?我们知道,掷硬币这个事件是服从伯努利分布的 Ber(p) , n次的伯努利实验就是我们熟知的二项分布 Bin(n,p), 这里的p就是一个参数,原来我们在做实验之前,这个参数就已经存在了(可以理解为上帝已经定好了),我们抽样出很多的样本 x 是为了找出这个参数,一个参数值。这个参数值必须通过大量的实验才能接近准确的。
贝叶斯的应用
现在到了贝叶斯的时间了。以前我们想知道一个参数,要通过大量的观测值才能得出,而现在运用了贝叶斯统计思想,这个后验概率分布 π(θ|x)其实是一系列参数值 θ 的概率分布,再说简单点就是我们得到了许多个参数 θ 及其对应的可能性,我们只需要从中选取我们想要的值就可以了。先验分布就是你在取得实验观测值以前对一个参数概率分布的 主观判断,这也就是为什么贝叶斯统计学一直不被认可的原因,频率学派认为统计学或者数学都是客观的,怎么能加入主观因素呢?但事实证明这样的效果会非常好!这其实跟我们人的思维方式一样,我们都是根据过往的经历,对事物有一定的信念跟判断,再根据判断结合一部分数据去预测下一步,而频率学派则完全根据过往的数据去判断,不带有任何主观因素。